
Career Boost: A Guide to RSA and How to Become A Cryptographer
- 8 minute read
-
Author: Mobica
In the exhilarating realm of cryptography and security, countless tech experts discover their true calling – a thrilling adventure into the unknown!
Many Mobicans can enthusiastically vouch for this, as our team has dozens of awesome security experts who have an unwavering passion for pioneering and developing next-generation hardware cryptography accelerators and implementing robust protocols for some of the biggest players in the semiconductor industry.
It’s what ignites our flame and sets us apart from the rest as we continue to deliver awesome security expertise to our customers.
But it's not all work and no play - Mobica has a thriving culture of learning and growth. From mentorship opportunities to a range of development programs, we're committed to helping Mobicans expand their skill sets and achieve their goals.
Many exciting possibilities lie ahead for aspiring security professionals. Whether you're interested in the intricacies of RSA, the power of elliptic curve cryptography, or the secrets of other asymmetric encryption algorithms, Mobica has the roles and projects to help you take your expertise to the next level.
In this article, we are taking a few minutes to geek out about the exciting possibilities of RSA, an encryption algorithm that allows for secure communication over the internet, afterwards, we will share how your cryptography aspirations can be actualised within Mobica. Including a list of things you can do to improve your cryptography expertise.
What is RSA?
Invented by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977, RSA has become one of the world's most widely used encryption systems, partly thanks to many readily available open-source implementations.
RSA is an example of an asymmetric encryption algorithm, which means that it uses different keys for encryption and decryption. The public key can be freely distributed and is used to encrypt or verify messages, while the private key is kept secret and is used to decrypt or sign them.
In simpler terms, RSA allows for secure communication by ensuring that only the intended recipient can read a message. This is achieved by encrypting the message with a public key that only the recipient has access to and decrypting it with a private key that only the recipient knows.
From this definition alone, we can already see how crucial this technology is for many use cases including data privacy.
Understanding congruence
To understand how RSA works, it's important to have a basic understanding of modular arithmetic. This is because RSA uses modular arithmetic to perform its encryption and decryption operations.
Modular arithmetic is a system of arithmetic where numbers "wrap around" after reaching a certain value. It's similar to a clock, where the numbers reset to zero after reaching twelve. In modular arithmetic, the number that the values "wrap around" to is called the modulus.
For example, if we consider the value 4 mod 7, it means that any number that leaves a remainder of 4 when divided by 7 is considered equivalent. We call such numbers congruent. This includes numbers like 11, 18, and so on. We denote this equivalence (congruency) with a triple-lined equality sign: 4 ≡ 11 (mod 7) ≡ 18 (mod 7)
In modular arithmetic, all numbers are within the range of 0 to the modulus minus one. For example, in the case of modulus 7, all numbers are between 0 and 6 inclusive.
The RSA principle
The RSA algorithm relies on the principle that it is easy to find a congruent value, but hard to determine the original value that was used initially. This forms the basis of RSA encryption, which can be expressed mathematically as:
(me)d ≡ m mod n
In this equation, e and d are integers, n is a product of two large prime numbers, and m is the message being encrypted.
The security of RSA encryption lies in the fact that, given only the values of e, n and m, it is infeasible to compute the value of d. This is because there is no known algorithm that can efficiently compute the modular inverse of a large number. Instead, it would require trying out every possible value of d, which is impractical for large numbers.
To make use of prime factorisation, RSA operates on large prime numbers. The choice of large prime numbers serves to constrain some of the operations and increase the difficulty of brute-force attacks. The larger the prime factors, the more secure the encryption.
Let’s try walking through an example with small numbers which you can easily verify even by hand.
Key generation
To generate an RSA key pair, we first choose two random prime numbers p and q that are similar in size. The use of prime numbers is important for the security of the algorithm.
p=13, q=17
Compute n=p*q
n =13*17=221
Compute least common multiple of (q-1,p-1):
l = lcm(q-1,p-1) = lcm(13-1,17-1) = lcm(12,16) = 48
Choose a number e in range 1<e<48 that is coprime (meaning their only common divisor is 1) with 48.
Let e=5
Find d such that
1 ≡ (e*d) mod l ≡ (5*d) mod 48 ≡ (5*29) mod 48 ≡ 145 mod 48
Finding d can be done using the extended Euclidean algorithm.
In our example the public key is (n=221,e=5) and the private key is (n=221,d=29).
Encryption and decryption
Using the equation from “The RSA principle” paragraph, lets encrypt a sample message m=22
me mod n ≡ 225 mod 221 ≡ 5153632 mod 221 ≡ 133
And decrypt it
(me)d mod n ≡ 13329 mod 221 ≡
≡39056883657367139614227739052562278609342949109376229274301653 mod 221 ≡ 22
In practice, computers can perform modular arithmetic efficiently using specialised algorithms that take advantage of the structure of the problem. The Chinese remainder theorem is one such algorithm, but there are others as well.
Signing and verification
We can use the same algorithm to sign and verify a message. This reverses how the keys are used: we sign messages with a private key and verify signatures with a public key.
Let’s create a signature s of the same message m=22 using our private key:
s = md mod n ≡ 2229 mod 221 ≡ 851643319086537701956194499721106030592 mod 221 ≡ 3
And verify this signature:
se mod n ≡ 35 mod 221 ≡ 243 mod 221 = 22 = m
In practice, we usually don’t sign the messages themselves, but rather their hashes (such as SHA1).
RSA summary
Overall, RSA is a widely used encryption algorithm that ensures secure communication over insecure channels. As you can see, the calculation of RSA keys and their utilisation is quite simple and can be done quickly on modern computers. In our example, we used small numbers to perform calculations easily, while in practice RSA uses 4096-bit long keys, which means values p and q each are 4096/2=2048 bits long.
Sample values for real-world RSA 4096 key:
p = 26877696304229263203762297021809521924258730081310102622008161734950647333823531661916229305077222858518814654799151936237572424790718073569976860971167104868754892446213551457284252643679953862869626257659200613607127760462008330323346511025408926035821557896067207636342343860619295883809666499802011467534457367542319669070214610709004089386353924049086521925221161044744243220322188232411524004385329446480306447426767087236062555325796237277256724406490689349643898889947850964321855749541008690860574588153950388150524982702943524177510790687478563406867856307265514974386816611748637617128241027641702852617449
q = 23112459363445999507451421610658109416782613715606548013446605994682944122318940405115241419658353901622634534934871741185778938878091108731416652598938930864035410146739250405065757183507930728905115084684054371884917111082591389859381221246193728945788849669203160202619608469340106177530038308133739719953032980713394013652585833483484129293999938445559660622882150706650769670490838152710377833982628691858024497817076970322410591926239300709378670463939782430766846383590629509640348413074637974435885387952644089114726363091079746263952890034441487247144806278553866465995702780628800382174657060405971375671359
Each a prime with 617 digits
Practical applications of RSA
Where RSA is being used? One of the primary applications is the encryption of messages, but with supply chain security tightening we can encounter it in more and more places, such as firmware update verification, HTTP encryption, VPNs, secure emails, document signatures, and online gaming.
Online gaming example
An example of RSA application can be found in online gaming, where a game can implement a system in which each user gets a generated unique private and public key pair which form the user's identity. Such identity can be readily transferred to the user’s other clients (computers) as it is stored as a key file in the industry standard PEM (Privacy-Enhanced Mail) format.
User willing to connect their client to a remote server for the first time first requests a token (nonce, a one-time, random stream of bytes) from the server. Server sends and remembers the token sent to each client. Upon receiving the token it is signed by the client using its private key and the signature is sent to the server together with the public key. Server validates the signature and if it is correct, the client is granted access.
An authorised client can be assigned to a group and each group carries a set of permissions for performing actions in the game. Assigning to a group equates to storing the client’s public key in a server-local database.
Authenticated client re-connecting to a server follows a similar path: a token is requested from the server, gets signed and sent back signed to the server. Server performs a lookup of the key in the local database and when a match is found, the client is automatically assigned to its previous group.
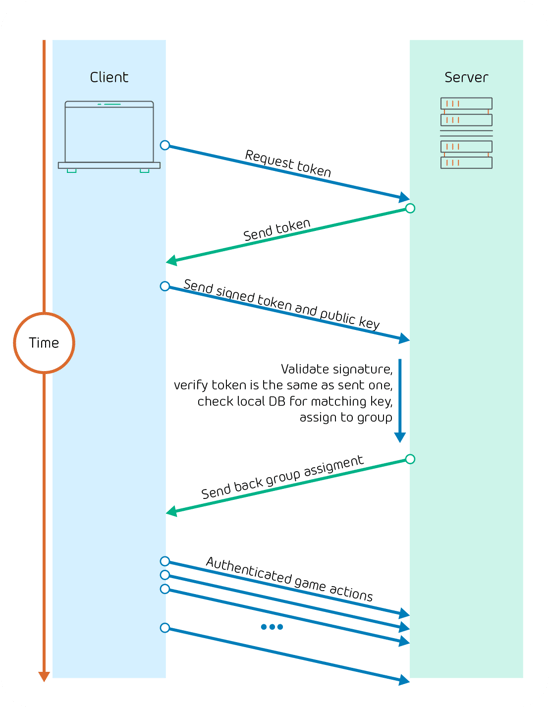
The token discussed earlier must be randomly generated each time to prevent a replay attack, where an adversary could intercept encrypted content and replay encrypted communication to gain authorised access without actually owning the private key.
As a long-time member of the OpenRCT2 project, I designed and implemented the scenario described above, which enables persistent and passwordless access to user-hosted servers. Contributing to multiple open source projects is not only a fun and fulfilling way to expand my expertise, but it also widens my perspective by letting me assume different roles: a feature developer, a product owner, a tutor for university students, a DevOps engineer, a community liaison, a user. Those skills transfer well from open source to commercial projects and help locate issues quicker, understand the broader scope and thus provide better solutions.
The drawback of this method is having to distribute the user's key to each server individually.
PKI
Mechanisms for key distribution, revocation, verification of entities owning keys, and certificate authorities (CA) are known as Public Key Infrastructure (PKI) and facilitate the trust.
In the scenario above we could envision a CA, where a user could register themselves, upload their public key and gain the trust of community peers. When vouched for, servers could be configured to query such service for connecting public keys and remove the need for initial group assignment in lieu of it happening automatically.
Multiple independent CAs can be established and they can be entrusted with varying levels of authority.
In a similar vein, a CA-less system can be established based purely on peers attesting to the authenticity of each other (e.g. by arranging a meeting and verifying IDs). Such systems are known as “web of trust” and are commonly employed e.g. in Linux distributions or package repositories such as NPM or PyPI.
Other ASYM cryptography
RSA is not the only algorithm for asymmetric cryptography. Another popular algorithm is elliptic curve cryptography or ElGamal, which employs other mathematical properties that come with different tradeoffs.
While powerful and secure when implemented correctly, asymmetric cryptography comes at an increased computational cost compared to symmetric cryptography (such as AES, especially with enhanced CPU instructions). Due to this complexity, asymmetric cryptography is sometimes used together with symmetric cryptography. One such use case is an exchange of symmetric keys using an asymmetrically encrypted channel.
In conclusion here are a few things that can put you on the path to becoming a cryptographer as well as further your already blooming cryptography career.
How to become An Expert Cryptographer
Develop a strong foundation in mathematics
As RSA relies heavily on mathematical concepts like modular arithmetic, it's essential to have a solid understanding of these topics. Take courses in number theory, algebra, and discrete mathematics to build a strong foundation.
Gain expertise and hands-on experience in cryptography
Have a deep understanding of encryption and decryption techniques to become an RSA cryptographer. Learn about various encryption algorithms, including symmetric and asymmetric cryptography, and explore their strengths and weaknesses.
Participate in Projects (Including open-source)
Participate in cryptography-related projects and competitions to gain practical experience. You can also work on open-source projects related to cryptography to improve your skills and gain exposure to different use cases.
Pursue relevant certifications
Earning industry-recognised certifications such as Certified Information Systems Security Professional (CISSP) and Certified Ethical Hacker (CEH) can help demonstrate your expertise in cryptography and security.
Network with industry professionals
Attend networking events and conferences to connect with professionals in the field. Join relevant groups and online communities to exchange ideas, learn from others, and stay updated with the latest industry news.

Consider joining Mobica
At Mobica, we specialise in delivering cutting-edge solutions in cryptography and security. Our team of experts helps customers across a wide range of industries, including semiconductor manufacturing, automotive, and fin-tech, to develop hardware cryptography accelerators and implement robust security protocols.
For instance, we work closely with a large semiconductor manufacturer to create firmware for their cryptographic coprocessors. Our support ranges from firmware development to the level of native microcode, ensuring that the coprocessors operate at peak performance and security.
We also collaborate with another major player in the semiconductor industry to develop parts of their open-source security protocol implementation. This work involves in-depth knowledge of the latest cryptographic techniques and protocols to create secure and efficient solutions.
While cryptography and security may be less prominent in some of our other projects and domains, we still apply our expertise to ensure that our customers' solutions are secure and compliant with industry standards.
Join the ranks of Mobica today and become part of a team that's pushing the limits of what's possible in the world of cryptography and security. The possibilities are endless, and the future is waiting to be unlocked.
Explore Our Career openings below.
Are you ready to make your own contribution?
Get started with Mobica today!
Contributor:
Michał Janiszewski
Principal Engineer, Middleware Competence Centre at Mobica

Michał is a principal engineer at Mobica with over 10 years of experience. His areas of expertise include C++ and Linux, successfully used in projects related to IVI, silicon validation, GPU drivers, DevOps. As open source contributor he is always on the lookout for upcoming technologies and how Mobica can deliver added value there.


